境界要素法による外部ポテンシャル場の計算
概要
このコラムでは、外部ポテンシャル場を境界要素法で扱う。線形の自己随伴演算子\(L\)に対して,グリーンの積分定理から,
\[
\int_{\Omega} \left[ \phi L G - G L \phi \right] \, d\Omega
= \int_{\Gamma_w} \left[ \phi \frac{\partial G}{\partial n} - G \frac{\partial \phi}{\partial n} \right] \, d\Gamma_w
\]
が成り立つ.
ここで,
\( \frac{\partial}{\partial n} \)
は,\(\Omega\)の外向き法線方向微分,
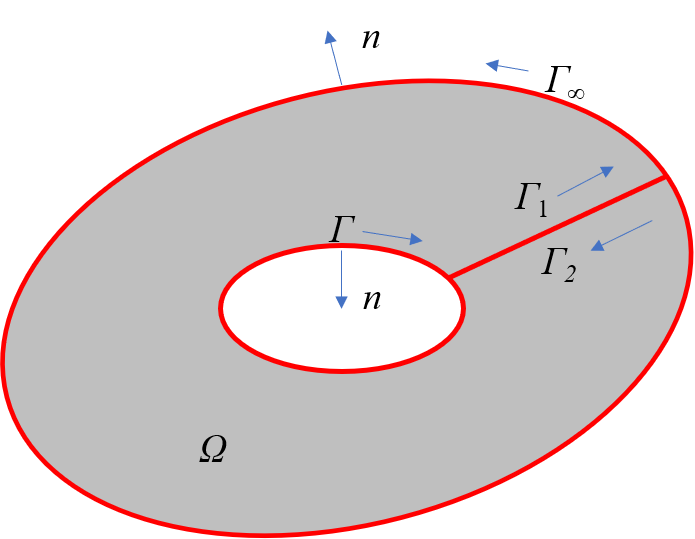
\(\Gamma_w\)は\(\Omega\)を(半時計回りCCWに)囲む閉曲線.
\(\Gamma_w\)を以下のように分割する:
\[ \Gamma_w = \Gamma + \Gamma_1 + \Gamma_\infty + \Gamma_2 \]
ここで, \(\Gamma\)は物体の外周,\(\Gamma_\infty\)は無限遠で\(\Omega\)を囲む積分路,\(\Gamma_{1,2}\)は,\( \Gamma \)と\(\Gamma_\infty\)をつなぐ連絡路.
\(\Gamma_{1,2}\)は同じ経路を逆向きに積分しているので,
\[
\int_{\Gamma_1+\Gamma_2} \left[ ...\right] \, d\Gamma =0
\]
無限遠方に設けた積分路において,
\[
\int_{\Gamma_\infty} \left[ ...\right] \, d\Gamma =0
\]
が成り立っていると仮定すると、積分路として\(\Gamma\)のみを考えればよく,この場合,
\[
\int_{\Omega} \left[ \phi L G - G L \phi \right] \, d\Omega
= \int_{\Gamma} \left[ \phi \frac{\partial G}{\partial n} - G \frac{\partial \phi}{\partial n} \right] \, d\Gamma
\]
が成り立つ.
問題として:
\[
L \phi=0
\]
を解くことを考える.ある特殊な関数\(G\)(基本解)があって,
\[
\int_{\Omega}\phi LG d\Omega = c \phi(r)
\]
あるいは,
\[
L G(r,r_0)= c \delta(r-r_0)
\]
が成り立つものとする.基本解を用いることで,左辺の積分は\(c\phi(r)\)になるので,\(r\in \Omega\)に対しては:
\[
c \phi(r)= \int_{\Gamma} \left[ \phi \frac{\partial G}{\partial n} - G \frac{\partial \phi}{\partial n} \right] \, d\Gamma
\]
が成り立つ.一方 \(r \in \Gamma\)に対しては,
\[
\theta c \phi(r)= \int_{\Gamma} \left[ \phi \frac{\partial G}{\partial n} - G \frac{\partial \phi}{\partial n} \right] \, d\Gamma
\]
となる.ここで\(\theta \in [0,1]\) は境界が特異点を横切る際の角度変化に依存するパラメータであり,
特異点を横切る境界が接線を有する十分に滑らか曲線であれば1/2になる.
さらに遠方場が既知であるとする.場の関数を遠方場と物体が存在することによる補正場の和として,
\[
\phi=\phi_\infty + \phi_c
\]
と仮定する.
このようにすることで,
\(\phi_c\)に関する無限遠に設けた閉曲線での積分がゼロになることが期待できる.
これを\(\phi\)に代入して,評価点\(r\)を\(\Gamma\)上にとる.未知数を左辺,既知の量を右辺にまとめると,
\[
\theta c \phi_c - \int_{\Gamma} \left[ \phi_c \frac{\partial G}{\partial n} - G \frac{\partial \phi_c}{\partial n} \right] \, d\Gamma
=-\theta c \phi_\infty + \int_{\Gamma} \left[ \phi_\infty \frac{\partial G}{\partial n} - G \frac{\partial \phi_\infty}{\partial n} \right] \, d\Gamma
\]
が得られる.これを離散化して,線形方程式にまとめる.
未知変数を
\[
\Phi=
\left[
\phi_0, \phi_1,...\phi_{N-1} ,
\frac{\partial\phi}{\partial n}_0,
\frac{\partial\phi}{\partial n}_1,
...,
\frac{\partial\phi}{\partial n}_{N-1}
\right]^T
\]
とする。\(\Phi\)の係数行列\(A\)を
\[
A=
\begin{bmatrix}
\theta c E & 0 \\
0 & 0
\end{bmatrix}
+
\begin{bmatrix}
-\frac{\partial G}{\partial n} & G \\
0 & 0
\end{bmatrix}
+
\begin{bmatrix}
0 & 0 \\
0 & E
\end{bmatrix}
\]
と定義すると、
\[
A \Phi_c = -A \Phi_\infty
\]
となる.これを解くことで,境界上の\(\phi_c\), \(\frac{\partial \phi_c}{\partial n} \)が得られる.
なお,\(A\)の第3項は,物体表面ではポテンシャルの法線方向微分がゼロ,すなわち:
\[
\frac{\partial \phi}{\partial n} =\frac{\partial \phi_\infty}{\partial n}+\frac{\partial \phi_c}{\partial n}=0
\]
という無通過条件に対応している.
\(\Omega\)内の点\(r\)におけるポテンシャル\(\phi(r)\)は:
\[
\phi(r)
=\phi_\infty(r)+\phi_c(r)
=\phi_\infty(r)
+
\frac{1}{c}
\int_{\Gamma} \left[ \phi_c \frac{\partial G}{\partial n} - G \frac{\partial \phi_c}{\partial n} \right] \, d\Gamma
\]
として求めることができる.
ラプラシアンに対する基本解の定義は,数学と工学で流儀があるようで,工学では\(c=-1\)とすることが多い.
これは工学で扱う問題が生成項を\(\rho\)とした時,場の方程式が,
\[
L \phi+\rho=0
\]
のような保存則から導かれることが多いことに起因する.
この時,\(\phi\)を
\[
\phi = \int_\Omega G \rho d\Omega + \int_\Gamma[...]d\Gamma
\]
のように書きたい思うのは自然な流れで,その場合,基本解\(G\)は,
\[
L G = -\delta
\]
と,マイナスの符号が付加された形で定義される.
計算例
以下では,正方形形状の物体を一様流中に置いたときのポテンシャル流れを,境界要素法(BEM)により解析する.
解析領域は,物体の外部空間であり,ラプラス方程式
\[
\nabla^2 \phi = 0
\]
を満たすポテンシャル \(\phi\) を,物体表面に課される無通過条件のもとで数値的に求める.
ポテンシャルは一様流のポテンシャル \(\phi_\infty\) と,物体の存在により生じる補正ポテンシャル \(\phi_c\) に分解される:
\[
\phi = \phi_\infty + \phi_c
\]
BEMにより,物体の外周に配置された離散パネル上での \(\phi_c\) およびその法線方向微分 \(\partial \phi_c / \partial n\) を求める.
以下の図は,物体まわりのポテンシャル分布を可視化したものであり,一様流が物体によってどのように変形されるかが示されている:
行列のヒートマップ
BEMにより構成される係数行列 \(A\) の構造を,絶対値のスケーリングで可視化することで,系の対称性やスパース性の情報を確認できる:
無限遠における補正ポテンシャルの減衰
この例題では「無限遠での積分項は0である」と仮定しているが,これが数値的に正当化されるかを確認することは重要である.
ここでは,物体から離れた位置(例:\(x=R, y=0\))において,
積分項
\[
\phi_c \cdot \frac{\partial G}{\partial n}, \quad
\frac{\partial \phi_c}{\partial n} \cdot G
\]
がどのようなオーダーで減衰するかを評価し,それぞれに積分路の長さスケーリング \(R\) を掛けた量をプロットする.
これにより,積分
\[
\int_{\Gamma_\infty} \left( \phi_c \frac{\partial G}{\partial n} - G \frac{\partial \phi_c}{\partial n} \right) d\Gamma
\]
が \(R \to \infty\) で消失するかを検証する.積分路は\(R\)のオーダーで大きくなるので,
\(R \cdot |\phi_c \cdot \partial G / \partial n|\)
および、
\(R \cdot |\partial \phi_c/\partial n \cdot G |\)
を評価する.\(x=R,y=0\)を代表点として計算すると,以下の結果が得られる.
この図から,
\(R \cdot |\phi_c \cdot \partial G / \partial n|\)
および、
\(R \cdot |\partial \phi_c/\partial n \cdot G |\)
のいずれもが\(R\)の増大に伴い減衰しており,\(\int_{\Gamma_\infty} d\Gamma \)が無視できることがわかる.
プログラムコード
Fuijta@PARI(2025)