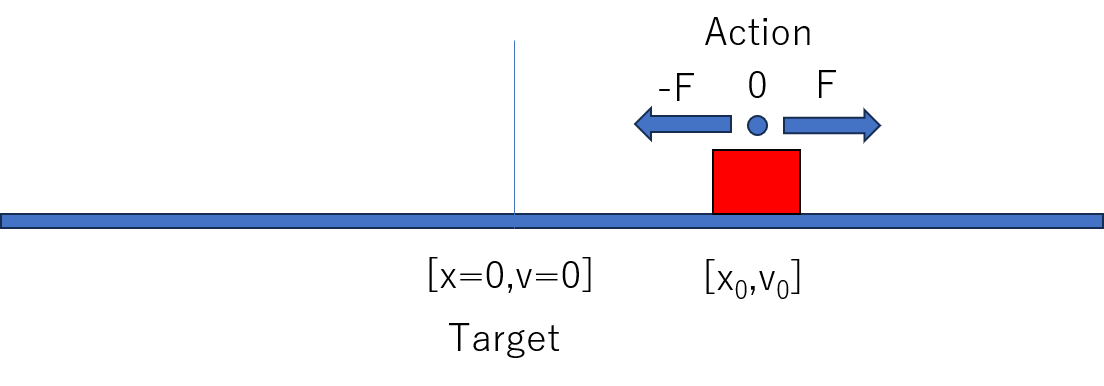
強化学習における「Actor-Critic」法を用いて、1 次元上の物体を原点に静止させる問題を学習します。 状態は連続(位置と速度)、行動は離散(加える力の選択)であり、 時間発展に従って状態価値関数と方策がどのように変化するかを可視化します。

再生時,ヒートマップ上をクリックすると初期状態を指定できます
状態 $s = (x, \dot{x})$ において離散的な力 $a \in \{-f, 0, +f\}$ を選択する問題を考えます。 状態価値関数 $V(s)$ は以下の TD 誤差をもとに更新されます:
$$ \delta = r + \gamma V(s') - V(s) $$ここで $\gamma$ は割引率、$r$ は報酬です。 Critic は $V(s)$ を重み付き2次関数としてモデル化し、$\delta$ に従って係数を更新します。
このデモでは、状態 \( s = (x, \dot{x}) \) に対する価値関数 \( V(s) \) を以下の2次式で表現しています:
$$ V(s) = w_1 x + w_2 \dot{x} + w_3 x^2 + w_4 \dot{x}^2 + w_5 x \dot{x} $$単なる線形結合や2乗項だけでは、原点に近づく動きと遠ざかる動きの違いを捉えることができません。 交差項 \( x \dot{x} \) を加えることで、 「原点に向かう状態(\( x \dot{x} < 0 \))」を高く評価し、 「遠ざかる状態(\( x \dot{x} > 0 \))」を低く評価するような分布が学習可能になります。
一方、Actor はソフトマックスにより行動確率 $\pi(a|s)$ を決定します。 $\pi(a|s)$ は $s$ に対する線形関数で構成されており、$\delta$ の符号に応じてその重みを調整します。
Critic(状態価値関数)は、状態 \( s \) における価値を次のような線形モデルで近似しています:
$$ V(s; w) = w^\top \phi(s) $$強化学習では、状態遷移 \( s \rightarrow s' \) における報酬 \( r \) を受けて、以下のような TD 誤差(Temporal Difference Error)を定義します:
$$ \delta = r + \gamma V(s'; w) - V(s; w) $$この誤差を最小化するために、以下のような損失関数を考えます:
$$ \mathcal{L}(w) = \frac{1}{2} \delta^2 = \frac{1}{2} \left( r + \gamma V(s'; w) - V(s; w) \right)^2 $$厳密にはこの損失の勾配は次のようになります:
$$ \nabla_w \mathcal{L} = \delta \cdot \left( \gamma \nabla_w V(s'; w) - \nabla_w V(s; w) \right) $$しかし、実際の Actor-Critic の学習では、semi-gradient(半勾配)という近似を用いて、次のように簡略化します:
$$ \nabla_w \mathcal{L} \approx -\delta \cdot \nabla_w V(s; w) = -\delta \cdot \phi(s) $$これは「将来の価値 \( V(s') \) は固定されたターゲットであり、学習の対象としない」とすることで、 勾配計算を簡単にし、学習の安定性を高める手法です。
したがって、パラメータ更新式は次のように表されます:
$$ w \leftarrow w + \alpha \cdot \delta \cdot \phi(s) $$この更新は、損失を最小にする方向(勾配の負方向)に沿って進むものであり、 実装においては以下のようなコードとして表現されます:
for (let i = 0; i < w.length; i++) {
w[i] += alpha * td * phi[i];
}
方策パラメータ \( w \) による目的関数 \( J(s) \) の勾配を次のように定義します:
$$ J(s) = \int \pi(a|s) \cdot Q^{\pi}(s, a) \, da $$この関数の勾配をとります:
$$ \nabla_w J(s) = \nabla_w \int \pi(a|s) \cdot Q^{\pi}(s, a) \, da $$積分の中に勾配を入れます(微分と積分の交換):
$$ = \int \nabla_w \pi(a|s) \cdot Q^{\pi}(s, a) \, da $$ここで対数微分の恒等式 \( \nabla_w \pi = \pi \cdot \nabla_w \log \pi \) を使うと:
$$ = \int \pi(a|s) \cdot \nabla_w \log \pi(a|s) \cdot Q^{\pi}(s, a) \, da $$これは確率分布 \( \pi(a|s) \) に関する期待値の形になります:
$$ = \mathbb{E}_{a \sim \pi} \left[ \nabla_w \log \pi(a|s) \cdot Q^{\pi}(s, a) \right] $$Actor-Critic 法では \( Q^{\pi}(s, a) \) を TD誤差で近似します:
$$ \delta = r + \gamma V(s') - V(s) $$よって、最終的に以下のように近似されます:
$$ \nabla_w J(s) \approx \mathbb{E}_{a \sim \pi} \left[ \nabla_w \log \pi(a|s) \cdot \delta \right] $$実際に選択した行動 \( a \) に基づいて、期待値については次のように一サンプルで近似できます:
$$ \nabla_w J(s) \approx \nabla_w \log \pi(a|s) \cdot \delta $$状態 \( s = (x, \dot{x}) \) に対して、各行動 \( a_i \) に対応するスコア(logit)を 重みベクトル \( w_i = [w_{i1}, w_{i2}] \) を用いて以下のように定義します:
$$ z_i = w_{i1} x + w_{i2} \dot{x} = w_i^\top s $$行動 \( a_i \) を選ぶ確率(softmax)は次のようになります:
$$ \pi(a_i|s) = \frac{\exp(z_i)}{\sum_j \exp(z_j)} $$方策勾配法では \( \nabla_w \log \pi(a|s) \) を求める必要があります。 まず、\(\pi(a_k|s)\) の対数をとります(\(a_k\) が選択された行動):
$$ \log \pi(a_k|s) = z_k - \log \sum_j \exp(z_j) $$これを \( w_k \) で微分すると:
$$ \nabla_{w_k} \log \pi(a_k|s) = \nabla_{w_k} z_k - \nabla_{w_k} \log \sum_j \exp(z_j) $$第一項は:
$$ \nabla_{w_k} z_k = \nabla_{w_k}(w_k^\top s) = s $$第二項はチェーンルールにより:
$$ \nabla_{w_k} \log \sum_j \exp(z_j) = \sum_j \frac{\exp(z_j)}{\sum_j \exp(z_j)} \cdot \nabla_{w_k} z_j $$ただし、\( \nabla_{w_k} z_j = 0 \) for \( j \ne k \)、および \( \nabla_{w_k} z_k = s \) なので、
$$ \nabla_{w_k} \log \sum_j \exp(z_j) = \pi(a_k|s) \cdot s $$ ---以上より:
$$ \nabla_{w_k} \log \pi(a_k|s) = s - \pi(a_k|s) \cdot s = (1 - \pi(a_k|s)) \cdot s $$同様に、\( w_j \) に関する勾配(選ばれなかった行動)も計算できます:
$$ \nabla_{w_j} \log \pi(a_k|s) = - \pi(a_j|s) \cdot s \quad \text{for } j \ne k $$全体をまとめると、各行動 \( a_j \) に対応する重み \( w_j \) に対する勾配は:
$$ \nabla_{w_j} \log \pi(a_k|s) = \begin{cases} (1 - \pi(a_k|s)) \cdot s & \text{if } j = k \\\\ - \pi(a_j|s) \cdot s & \text{if } j \ne k \end{cases} $$TD誤差 \( \delta \) を使った方策勾配法では、以下のように更新されます:
$$ w_j \leftarrow w_j + \alpha \cdot \delta \cdot \nabla_{w_j} \log \pi(a_k|s) $$実装を簡潔にするために、今回のデモでは以下のような簡略化近似を採用しています:
$$ \nabla_{w_k} \log \pi(a_k|s) \approx s $$この近似のもとで、選択された行動 \( a_k \) に対してのみ次のように重みを更新します:
$$ w_k \leftarrow w_k + \alpha \cdot \delta \cdot s $$これがプログラム中の以下の実装と一致しています:
actor.update = function(s, aIdx, td, alpha) {
this.w[aIdx][0] += alpha * td * s.x;
this.w[aIdx][1] += alpha * td * s.v;
}
以下はブラウザ上で動作している学習アルゴリズムのスクリプト本体です。